Thursday, August 28, 2014

BIOINFORMATICS PART 2


Artificial neural network


An artificial neural network, often just called a neural network, is a mathematical model inspired by biological neural networks. A neural network consists of an interconnected group of
artificial neurons, and it processes information using a connectionist approach to computation. In most cases a neural network is an adaptive system that changes its structure during a learning phase. Neural networks are used to model complex relationships between inputs and outputs or to
find patterns in data.

Network function

The word network in the term 'artificial neural network' refers to the inter–connections between the neurons in the different layers of each system. An example system has three layers. The first layer has input neurons, which send data via synapses to the second layer of neurons, and then via more synapses to the third layer of output neurons. More complex systems will have more layers of neurons with some having increased layers of input neurons and output neurons. The synapses store parameters called "weights" that manipulate the data in the calculations.
An ANN is typically defined by three types of parameters:
  1. The interconnection pattern between different layers of neurons
  2. The learning process for updating the weights of the interconnections
  3. The activation function that converts a neuron's weighted input to its output activation.

Employing artificial neural networks

Perhaps the greatest advantage of ANNs is their ability to be used as an arbitrary function approximation mechanism that 'learns' from observed data. However, using them is not so straightforward and a relatively good understanding of the underlying theory is essential.
  • Choice of model: This will depend on the data representation and the application. Overly complex models tend to lead to problems with learning.
  • Learning algorithm: There are numerous trade-offs between learning algorithms. Almost any algorithm will work well with the correct hyperparameters for training on a particular fixed data set. However selecting and tuning an algorithm for training on unseen data requires a significant amount of experimentation.
  • Robustness: If the model, cost function and learning algorithm are selected appropriately the resulting ANN can be extremely robust.
With the correct implementation, ANNs can be used naturally in
online learning and large data set applications. Their simple implementation and the existence of mostly local dependencies exhibited in the structure allows for fast, parallel implementations in hardware.

[edit] Applications

The utility of artificial neural network models lies in the fact that they can be used to infer a function from observations. This is particularly useful in applications where the complexity of the data or task makes the design of such a function by hand impractical.

[edit] Real-life applications

The tasks artificial neural networks are applied to tend to fall within the following broad categories:
Application areas include system identification and control, quantum chemistry,[7] game-playing and decision making (backgammon, chess, poker), pattern recognition (radar systems, face identification, object recognition and more), sequence recognition, medical diagnosis, financial applications (automated trading systems), data mining (or knowledge discovery in databases, "KDD"), visualization and
e-mail spam filtering.

[edit] Neural networks and neuroscience

Theoretical and computational neuroscience is the field concerned with the theoretical analysis and computational modeling of biological neural systems. Since neural systems are intimately related to cognitive processes and behavior, the field is closely related to cognitive and behavioral modeling.
The aim of the field is to create models of biological neural systems in order to understand how biological systems work. To gain this understanding, neuroscientists strive to make a link between observed biological processes (data), biologically plausible mechanisms for neural processing and learning (biological neural network models) and theory (statistical learning theory and information theory).


















Natural language processing

Natural language processing (NLP) is a field of
computer science, artificial intelligence, and linguistics concerned with the interactions between computers and
human (natural) languages. As such, NLP is related to the area of human–computer interaction. Many challenges in NLP involve natural language understanding -- that is, enabling computers to derive meaning from human or natural language input.

[edit] Major tasks in NLP

The following is a list of some of the most commonly researched tasks in NLP. Note that some of these tasks have direct real-world applications, while others more commonly serve as subtasks that are used to aid in solving larger tasks. What distinguishes these tasks from other potential and actual NLP tasks is not only the volume of research devoted to them but the fact that for each one there is typically a well-defined problem setting, a standard metric for evaluating the task, standard corpora on which the task can be evaluated, and competitions devoted to the specific task.
  • Automatic summarization: Produce a readable summary of a chunk of text. Often used to provide summaries of text of a known type, such as articles in the financial section of a newspaper.
  • Machine translation: Automatically translate text from one human language to another.
  • Natural language generation: Convert information from computer databases into readable human language.
  • Optical character recognition (OCR): Given an image representing printed text, determine the corresponding text.
  • Parsing: Determine the parse tree (grammatical analysis) of a given sentence. The grammar for
    natural languages is ambiguous and typical sentences have multiple possible analyses.
  • Question answering: Given a human-language question, determine its answer. Typical questions have a specific right answer (such as "What is the capital of Canada?"), but sometimes open-ended questions are also considered (such as "What is the meaning of life?").
  • Relationship extraction: Given a chunk of text, identify the relationships among named entities (e.g. who is the wife of whom).
  • Sentence breaking (also known as sentence boundary disambiguation): Given a chunk of text, find the sentence boundaries. Sentence boundaries are often marked by periods or other punctuation marks, but these same characters can serve other purposes (e.g. marking abbreviations).
  • Sentiment analysis: Extract subjective information usually from a set of documents, often using online reviews to determine "polarity" about specific objects. It is especially useful for identifying trends of public opinion in the social media, for the purpose of marketing.
In some cases, sets of related tasks are grouped into subfields of NLP that are often considered separately from NLP as a whole. Examples include:
Other tasks include:












BLAST

In bioinformatics, Basic Local Alignment Search Tool, or BLAST, is an algorithm for comparing primary biological sequence information, such as the amino-acid sequences of different proteins or the nucleotides of
DNA sequences. A BLAST search enables a researcher to compare a query sequence with a library or database of sequences, and identify library sequences that resemble the query sequence above a certain threshold. Different types of BLASTs are available according to the query sequences. For example, following the discovery of a previously unknown gene in the mouse, a scientist will typically perform a BLAST search of the human genome to see if humans carry a similar gene; BLAST will identify sequences in the human genome that resemble the mouse gene based on similarity of sequence. The BLAST program was designed by
Stephen Altschul, Warren Gish, Webb Miller, Eugene Myers, and David J. Lipman at the NIH and was published in the Journal of Molecular Biology in 1990.[1]

[edit] Algorithm

To run, BLAST requires a query sequence to search for, and a sequence to search against (also called the target sequence) or a sequence database containing multiple such sequences. BLAST will find sub-sequences in the database which are similar to subsequences in the query. In typical usage, the query sequence is much smaller than the database, e.g., the query may be one thousand nucleotides while the database is several billion nucleotides.
The main idea of BLAST is that there are often high-scoring segment pairs (HSP) contained in a statistically significant alignment. BLAST searches for high scoring
sequence alignments between the query sequence and sequences in the database using a heuristic approach that approximates the Smith-Waterman algorithm. The exhaustive Smith-Waterman approach is too slow for searching large genomic databases such as GenBank. Therefore, the BLAST algorithm uses a
heuristic approach that is less accurate than the Smith-Waterman algorithm but over 50 times faster. The speed and relatively good accuracy of BLAST are among the key technical innovations of the BLAST programs.
An overview of the BLASTP algorithm (a protein to protein search) is as follows:[6]
  1. Remove low-complexity region or sequence repeats in the query sequence.
  2. Make a k-letter word list of the query sequence.
  3. List the possible matching words.
  4. Organize the remaining high-scoring words into an efficient search tree.
  5. Repeat step 3 to 4 for each k-letter word in the query sequence.
  6. Scan the database sequences for exact matches with the remaining high-scoring words.
  7. Extend the exact matches to high-scoring segment pair (HSP).
  8. List all of the HSPs in the database whose score is high enough to be considered.
  9. Evaluate the significance of the HSP score.
  10. Make two or more HSP regions into a longer alignment.
  11. Show the gapped Smith-Waterman local alignments of the query and each of the matched database sequences.
  12. Report every match whose expect score is lower than a threshold parameter E.

Uses of BLAST

BLAST can be used for several purposes. These include identifying species, locating domains, establishing phylogeny, DNA mapping, and comparison.
Identifying species
With the use of BLAST, you can possibly correctly identify a species and/or find homologous species. This can be useful, for example, when you are working with a DNA sequence from an unknown species.
Locating domains
When working with a protein sequence you can input it into BLAST, to locate known domains within the sequence of interest.
Establishing phylogeny
Using the results received through BLAST you can create a phylogenetic tree using the BLAST web-page. Phylogenies based on BLAST alone are less reliable than other purpose-built computational phylogenetic methods, so should only be relied upon for "first pass" phylogenetic analyses.
DNA mapping
When working with a known species, and looking to sequence a gene at an unknown location, BLAST can compare the chromosomal position of the sequence of interest, to relevant sequences in the database(s).
Comparison
When working with genes, BLAST can locate common genes in two related species, and can be used to map annotations from one organism to another







Molecular modelling

Molecular modeling encompasses all theoretical methods and computational techniques used to
model or mimic the behaviour of molecules. The techniques are used in the fields of computational chemistry, drug design, computational biology and
materials science for studying molecular systems ranging from small chemical systems to large biological molecules and material assemblies. The simplest calculations can be performed by hand, but inevitably computers are required to perform molecular modelling of any reasonably sized system. The common feature of molecular modelling techniques is the atomistic level description of the molecular systems. This may include treating atoms as the smallest individual unit (the
Molecular mechanics approach), or explicitly modeling electrons of each atom (the
quantum chemistry approach).

Molecular mechanics

Molecular mechanics is one aspect of molecular modelling, as it refers to the use of
classical mechanics/
Newtonian mechanics to describe the physical basis behind the models. Molecular models typically describe atoms (nucleus and electrons collectively) as point charges with an associated mass. The interactions between neighbouring atoms are described by spring-like interactions (representing
chemical bonds) and
van der Waals forces. The Lennard-Jones potential is commonly used to describe
van der Waals forces. The electrostatic interactions are computed based on
Coulomb's law. Atoms are assigned coordinates in Cartesian space or in internal coordinates, and can also be assigned velocities in dynamical simulations. The atomic velocities are related to the temperature of the system, a macroscopic quantity. The collective mathematical expression is known as a potential function and is related to the system internal energy (U), a thermodynamic quantity equal to the sum of potential and kinetic energies. Methods which minimize the potential energy are known as energy minimization techniques (e.g.,
steepest descent and
conjugate gradient), while methods that model the behaviour of the system with propagation of time are known as molecular dynamics.
E = E_\text{bonds} + E_\text{angle} + E_\text{dihedral} + E_\text{non-bonded} \,
E_\text{non-bonded} = E_\text{electrostatic} + E_\text{van der Waals} \,
This function, referred to as a
potential function, computes the molecular potential energy as a sum of energy terms that describe the deviation of bond lengths, bond angles and torsion angles away from equilibrium values, plus terms for non-bonded pairs of atoms describing van der Waals and electrostatic interactions. The set of parameters consisting of equilibrium bond lengths, bond angles, partial charge values, force constants and van der Waals parameters are collectively known as a force field. Different implementations of molecular mechanics use different mathematical expressions and different parameters for the
potential function. The common force fields in use today have been developed by using high level quantum calculations and/or fitting to experimental data. The technique known as energy minimization is used to find positions of zero gradient for all atoms, in other words, a local energy minimum. Lower energy states are more stable and are commonly investigated because of their role in chemical and biological processes. A
molecular dynamics simulation, on the other hand, computes the behaviour of a system as a function of time. It involves solving Newton's laws of motion, principally the second law, \mathbf{F} = m\mathbf{a}. Integration of Newton's laws of motion, using different integration algorithms, leads to atomic trajectories in space and time. The force on an atom is defined as the negative gradient of the potential energy function. The energy minimization technique is useful for obtaining a static picture for comparing between states of similar systems, while molecular dynamics provides information about the dynamic processes with the intrinsic inclusion of temperature effects.

[edit] Applications

Molecular modelling methods are now routinely used to investigate the structure, dynamics, surface properties and thermodynamics of inorganic, biological and polymeric systems. The types of biological activity that have been investigated using molecular modelling include
protein folding, enzyme catalysis, protein stability, conformational changes associated with biomolecular function, and molecular recognition of proteins, DNA, and membrane complexes















FASTA

FASTA is a DNA and protein
sequence alignment software package first described (as FASTP) by David J. Lipman and William R. Pearson in 1985.[1] Its legacy is the FASTA format which is now ubiquitous in bioinformatics.

Search method

FASTA takes a given nucleotide or amino-acid sequence and searches a corresponding sequence database by using local sequence alignment to find matches of similar database sequences.
The FASTA program follows a largely heuristic method which contributes to the high speed of its execution. It initially observes the pattern of word hits, word-to-word matches of a given length, and marks potential matches before performing a more time-consuming optimized search using a Smith-Waterman type of algorithm.
The size taken for a word, given by the parameter ktup, controls the sensitivity and speed of the program. Increasing the ktup value decreases number of background hits that are found. From the word hits that are returned the program looks for segments that contain a cluster of nearby hits. It then investigates these segments for a possible match.
There are some differences between fastn and fastp relating to the type of sequences used but both use four steps and calculate three scores to describe and format the sequence similarity results. These are:
  • Identify regions of highest density in each sequence comparison. Taking a ktup to equal 1 or 2.
  • Rescan the regions taken using the scoring matrices. trimming the ends of the region to include only those contributing to the highest score.
  • In an alignment if several initial regions with scores greater than a CUTOFF value are found, check whether the trimmed initial regions can be joined to form an approximate alignment with gaps. Calculate a similarity score that is the sum of the joined regions penalising for each gap 20 points. This initial similarity score (initn) is used to rank the library sequences. The score of the single best initial region found in step 2 is reported (init1).
  • Use a banded Smith-Waterman algorithm to calculate an optimal score for alignment.

Uses

FASTA is pronounced "fast A", and stands for "FAST-All", because it works with any alphabet, an extension of "FAST-P" (protein) and "FAST-N" (nucleotide) alignment.
The current FASTA package contains programs for protein:protein, DNA:DNA, protein:translated DNA (with frameshifts), and ordered or unordered peptide searches. Recent versions of the FASTA package include special translated search algorithms that correctly handle frameshift errors (which six-frame-translated searches do not handle very well) when comparing nucleotide to protein sequence data.
In addition to rapid heuristic search methods, the FASTA package provides SSEARCH, an implementation of the optimal Smith-Waterman algorithm.
A major focus of the package is the calculation of accurate similarity statistics, so that biologists can judge whether an alignment is likely to have occurred by chance, or whether it can be used to infer homology. The FASTA package is available from fasta.bioch.virginia.edu.
The web-interface to submit sequences for running a search of the European Bioinformatics Institute (EBI)'s online databases is also available using the FASTA programs.
The
FASTA file format used as input for this software is now largely used by other sequence database search tools (such as BLAST) and sequence alignment programs (Clustal, T-Coffee, etc.).





Clustering
What is Clustering?
Clustering can be considered the most important unsupervised learning problem; so, as every other problem of this kind, it deals with finding a structure in a collection of unlabeled data.
A loose definition of clustering could be “the process of organizing objects into groups whose members are similar in some way”.
A cluster is therefore a collection of objects which are “similar” between them and are “dissimilar” to the objects belonging to other clusters.
We can show this with a simple graphical example:
In this case we easily identify the 4 clusters into which the data can be divided; the similarity criterion is distance: two or more objects belong to the same cluster if they are “close” according to a given distance (in this case geometrical distance). This is called distance-based clustering.
Another kind of clustering is conceptual clustering: two or more objects belong to the same cluster if this one defines a concept common to all that objects. In other words, objects are grouped according to their fit to descriptive concepts, not according to simple similarity measures.
Possible Applications
Clustering algorithms can be applied in many fields, for instance:
  • Marketing: finding groups of customers with similar behavior given a large database of customer data containing their properties and past buying records;
  • Biology: classification of plants and animals given their features;
  • Libraries: book ordering;
  • Insurance: identifying groups of motor insurance policy holders with a high average claim cost; identifying frauds;
  • City-planning: identifying groups of houses according to their house type, value and geographical location;
  • Earthquake studies: clustering observed earthquake epicenters to identify dangerous zones;
  • WWW: document classification; clustering weblog data to discover groups of similar access patterns.
Requirements
The main requirements that a clustering algorithm should satisfy are:
  • scalability;
  • dealing with different types of attributes;
  • discovering clusters with arbitrary shape;
  • minimal requirements for domain knowledge to determine input parameters;
  • ability to deal with noise and outliers;
  • insensitivity to order of input records;
  • high dimensionality;
  • interpretability and usability.


Clustering Algorithms
Classification
Clustering algorithms may be classified as listed below:
  • Exclusive Clustering
  • Overlapping Clustering
  • Hierarchical Clustering
  • Probabilistic Clustering
In the first case data are grouped in an exclusive way, so that if a certain datum belongs to a definite cluster then it could not be included in another cluster. A simple example of that is shown in the figure below, where the separation of points is achieved by a straight line on a bi-dimensional plane.
On the contrary the second type, the overlapping clustering, uses fuzzy sets to cluster data, so that each point may belong to two or more clusters with different degrees of membership. In this case, data will be associated to an appropriate membership value.
Instead, a hierarchical clustering algorithm is based on the union between the two nearest clusters. The beginning condition is realized by setting every datum as a cluster. After a few iterations it reaches the final clusters wanted.
Finally, the last kind of clustering use a completely probabilistic approach.
In this tutorial we propose four of the most used clustering algorithms:
  • K-means
  • Fuzzy C-means
  • Hierarchical clustering
  • Mixture of Gaussians
Each of these algorithms belongs to one of the clustering types listed above. So that, K-means is an exclusive clustering algorithm, Fuzzy C-means is an overlapping clustering algorithm, Hierarchical clustering is obvious and lastly Mixture of Gaussian is a probabilistic clustering algorithm. We will discuss about each clustering method in the following paragraphs.








Protein structure prediction

Protein structure prediction is the prediction of the three-dimensional structure of a protein from its amino acid sequence — that is, the prediction of its secondary, tertiary, and quaternary structure from its primary structure. Structure prediction is fundamentally different from the inverse problem of
protein design. Protein structure prediction is one of the most important goals pursued by bioinformatics and theoretical chemistry; it is highly important in medicine (for example, in drug design) and biotechnology (for example, in the design of novel enzymes). Every two years, the performance of current methods is assessed in the CASP experiment (Critical Assessment of Techniques for Protein Structure Prediction).
Proteins are chains of amino acids joined together by peptide bonds. Many conformations of this chain are possible due to the rotation of the chain about each Cα atom. It is these informational changes that are responsible for differences in the three dimensional structure of proteins. Each amino acid in the chain is polar, i.e. it has separated positive and negative charged regions with a free C=O group, which can act as hydrogen bond acceptor and an NH group, which can act as hydrogen bond donor. These groups can therefore interact in the protein structure. The 20 amino acids can be classified according to the chemistry of the side chain which also plays an important structural role. Glycine takes on a special position, as it has the smallest side chain, only one Hydrogen atom, and therefore can increase the local flexibility in the protein structure. Cysteine on the other hand can react with another cysteine residue and thereby form a cross link stabilizing the whole structure.
The protein structure can be considered as a sequence of secondary structure elements, such as α helices and β sheets, which together constitute the overall three-dimensional configuration of the protein chain. In these secondary structures regular patterns of H bonds are formed between neighboring amino acids, and the amino acids have similar Φ and Ψ angles.
The formation of these structures neutralizes the polar groups on each amino acid. The secondary structures are tightly packed in the protein core in a hydrophobic environment. Each amino acid side group has a limited volume to occupy and a limited number of possible interactions with other near- by side chains, a situation that must be taken into account in molecular modeling and alignments. [1]

[edit] α Helix

The α helix is the most abundant type of secondary structure in proteins. The α helix has 3.6 amino acids per turn with an H bond formed between every fourth residue; the average length is 10 amino acids (3 turns) or 10 Å but varies from 5 to 40 (1.5 to 11 turns). The alignment of the H bonds creates a dipole moment for the helix with a resulting partial positive charge at the amino end of the helix. Because this region has free NH2 groups, it will interact with negatively charged groups such as phosphates. The most common location of α helices is at the surface of protein cores, where they provide an interface with the aqueous environment.

[edit] β Sheet

β Sheets are formed by H bonds between an average of 5–10 consecutive amino acids in one portion of the chain with another 5–10 farther down the chain. The interacting regions may be adjacent, with a short loop in between, or far apart, with other structures in between. Every chain may run in the same direction to form a parallel sheet, every other chain may run in the reverse chemical direction to form an anti parallel sheet, or the chains may be parallel and anti parallel to form a mixed sheet.

[edit] Loop

Loops are regions of a protein chain that are (1) between α helices and β sheets, (2) of various lengths and three-dimensional configurations, and (3) on the surface of the structure. Hairpin loops that represent a complete turn in the polypeptide chain joining two antiparallel β strands may be as short as two amino acids in length.

[edit] Coils

A region of secondary structure that is not a α helix, a β sheet, or a recognizable turn is commonly referred to as a coil.

Protein classification

Proteins may be classified according to both structural and sequence similarity. For structural classification, the sizes and spatial arrangements of secondary structures described in the above paragraph are compared in known three-dimensional structures.Classification based on sequence similarity was historically the first to be used. Initially, similarity based on alignments of whole sequences was performed. Later, proteins were classified on the basis of the occurrence of conserved amino acid patterns. Databases that classify proteins by one or more of these schemes are available. In considering protein classification schemes, it is important to keep several observations in mind. First, two entirely different protein sequences from different evolutionary origins may fold into a similar structure. Conversely, the sequence of an ancient gene for a given structure may have diverged considerably in different species while at the same time maintaining the same basic structural features. Recognizing any remaining sequence similarity in such cases may be a very difficult task. Second, two proteins that share a significant degree of sequence similarity either with each other or with a third sequence also share an evolutionary origin and should share some structural features also. However, gene duplication and genetic rearrangements during evolution may give rise to new gene copies, which can then evolve into proteins with new function and structure.[1]


[edit] Secondary structure

Secondary structure prediction is a set of techniques in bioinformatics that aim to predict the local secondary structures of proteins and RNA sequences based only on knowledge of their primary structure — amino acid or nucleotide sequence, respectively. For proteins, a prediction consists of assigning regions of the amino acid sequence as likely
alpha helices, beta strands (often noted as "extended" conformations), or
turns. The success of a prediction is determined by comparing it to the results of the
DSSP algorithm applied to the
crystal structure of the protein; for nucleic acids, it may be determined from the hydrogen bonding pattern. Specialized algorithms have been developed for the detection of specific well-defined patterns such as transmembrane helices and
coiled coils in proteins, or canonical microRNA structures in RNA.[1]
The best modern methods of secondary structure prediction in proteins reach about 80% accuracy;[2] this high accuracy allows the use of the predictions in
fold recognition and ab initio protein structure prediction, classification of
structural motifs, and refinement of
sequence alignments. The accuracy of current protein secondary structure prediction methods is assessed in weekly benchmarks such as LiveBench and EVA.

[edit] Tertiary structure

The practical role of protein structure prediction is now more important than ever. Massive amounts of protein sequence data are produced by modern large-scale DNA sequencing efforts such as the
Human Genome Project. Despite community-wide efforts in structural genomics, the output of experimentally determined protein structures—typically by time-consuming and relatively expensive
X-ray crystallography or NMR spectroscopy—is lagging far behind the output of protein sequences.

[edit] Quaternary structure

In the case of complexes of two or more proteins, where the structures of the proteins are known or can be predicted with high accuracy, protein–protein docking methods can be used to predict the structure of the complex. Information of the effect of mutations at specific sites on the affinity of the complex helps to understand the complex structure and to guide docking methods.






DNA microarray

A DNA microarray (also commonly known as DNA chip or biochip) is a collection of microscopic DNA spots attached to a solid surface. Scientists use DNA microarrays to measure the
expression levels of large numbers of genes simultaneously or to genotype multiple regions of a genome. Each DNA spot contains picomoles (10−12 moles) of a specific DNA sequence, known as probes (or reporters or oligos). These can be a short section of a gene or other DNA element that are used to hybridize a cDNA or cRNA (also called anti-sense RNA) sample (called target) under high-stringency conditions. Probe-target hybridization is usually detected and quantified by detection of fluorophore-, silver-, or chemiluminescence-labeled targets to determine relative abundance of nucleic acid sequences in the target.

Construction of the Arrays

To make the arrays, the sample DNA must be fixed onto glass microscope slides.

Microarray slides

DNA microarray slides are the slides that have the DNA sequences printed onto them robotically, in the specific grid pattern.
The surface-bound molecules are termed 'probes' because they are the molecules that probe, or interrogate the composition of the fluorescently labeled DNA population.
Methods of Construction
The construction of the microarrays involves laying the DNA onto the slide quickly, with a high degree of accuracy and reproducibility. There are a number of methods for producing the microarray slides, and these are mainly done using robotic systems.They each have their own advantages and disadvantages.
The 3 main methods for doing this are:
  1. Spotting of DNA fragments directly onto the slide,
  2. Arraying of prefabricated oligonucleotides, and
  3. In-situ synthesis of oligonucleotides, done on the chip.


Microspotting Techniques
The use of prefabricated oligonucleotides greatly simplifies the construction of microarrays. Conventional methods can be used to produce the sequences, and these can then be printed directly onto the microscope slide, which is first overlaid with a coating that is positively charged.
The cDNA or oligonucleotide material can be deposited straight from a reagent tray, where it is suspended in a denaturing solution, onto the glass surface by a printhead containing microspotting pins or micropipettes.
Piezoelectric Printing
Minute volumes of reagents are delivered to defined locations on the slide similar to 'ink-jet' printing methods.
The printhead moves across the array, and at each spot electrical stimulation causes the DNA bases, cDNAs or other molecules to be delivered onto the surface via tiny jets. This is a non-contact process.
Photolithography
The light from a mercury lamp activates modified photospecific versions of the four DNA bases. The photolithographic masks ensure the DNA synthesis is stimulated in defined positions - the masks predetermine which of the nucleotides are activated.
This 'in situ' fabrication technique was developed by Affymetrix, and is used to produce their GeneChips.
Working
The core principle behind microarrays is hybridization between two DNA strands, the property of complementary nucleic acid sequences to specifically pair with each other by forming hydrogen bonds between complementary nucleotide base pairs. A high number of complementary base pairs in a nucleotide sequence means tighter non-covalent bonding between the two strands. After washing off of non-specific bonding sequences, only strongly paired strands will remain hybridized. Fluorescently labeled target sequences that bind to a probe sequence generate a signal that depends on the hybridization conditions (such as temperature), and washing after hybridization. Total strength of the signal, from a spot (feature), depends upon the amount of target sample binding to the probes present on that spot. Microarrays use relative quantization in which the intensity of a feature is compared to the intensity of the same feature under a different condition, and the identity of the feature is known by its position.

Simulated annealing

Simulated annealing (SA) is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the
global optimum of a given function in a large search space. It is often used when the search space is discrete (e.g., all tours that visit a given set of cities). For certain problems, simulated annealing may be more efficient than
exhaustive enumeration — provided that the goal is merely to find an acceptably good solution in a fixed amount of time, rather than the best possible solution.
The name and inspiration come from annealing in metallurgy, a technique involving heating and controlled cooling of a material to increase the size of its crystals and reduce their defects, both are attributes of the material that depend on its thermodynamic free energy. Heating and cooling the material affects both the temperature and the thermodynamic free energy. While the same amount of cooling brings the same amount of decrease in temperature it will bring a bigger or smaller decrease in the thermodynamic free energy depending on the rate that it occurs, with a slower rate producing a bigger decrease.
This notion of slow cooling is implemented in the Simulated Annealing algorithm as a slow decrease in the probability of accepting worse solutions as it explores the solution space. Accepting worse solutions is a fundamental property of metaheuristics because it allows for a more extensive search for the optimal solution.

Overview

In the simulated annealing (SA) method, each point s of the search space is analogous to a state of some
physical system, and the function E(s) to be minimized is analogous to the
internal energy of the system in that state. The goal is to bring the system, from an arbitrary initial state, to a state with the minimum possible energy. Many commonly used mathematical terms have originated from this form of algorithm, notably 'achronotrope' which referrs to the behaviour of an alphabet key which has reached a local maximum.[citation needed]

[edit] The basic iteration

At each step, the SA heuristic considers some neighbouring state s' of the current state s, and probabilistically decides between moving the system to state s' or staying in state s. These probabilities ultimately lead the system to move to states of lower energy. Typically this step is repeated until the system reaches a state that is good enough for the application, or until a given computation budget has been exhausted.

[edit] The neighbours of a state

The neighbours of a state are new states of the problem that are produced after altering a given state in some particular way. For example, in the traveling salesman problem, each state is typically defined as a particular permutation of the cities to be visited. The neighbours of a permutation are the permutations that are produced, for example, by interchanging a pair of adjacent cities. The action taken to alter the solution in order to find neighbouring solutions is called a "move" and different moves give different neighbours. These moves usually result in minimal alterations of the solution, as the previous example depicts, in order to help an algorithm optimize the solution to the maximum extent while retaining the already optimum parts of the solution and affecting only the suboptimum parts. In the previous example, the parts of the solution are the city connections.

[edit] Acceptance probabilities

The probability of making the
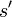transition from the current state sto a candidate new state s'is specified by an acceptance probability function P(e, e', T), that depends on the energies e = E(s)and e' = E(s')of the two states, and on a global time-varying parameter Tcalled the temperature. States with a smaller energy are better than those with a greater energy. The probability function Pmust be positive even when e'is greater than e. This feature prevents the method from becoming stuck at a local minimum that is worse than the global one.

[edit] The annealing schedule

The name and inspiration of the algorithm demand an interesting feature related to the temperature variation to be embedded in the operational characteristics of the algorithm. This necessitates a gradual reduction of the temperature as the simulation proceeds. The algorithm starts initially with Tset to a high value (or infinity), and then it is decreased at each step following some annealing schedule—which may be specified by the user, but must end with T=0towards the end of the allotted time budget. In this way, the system is expected to wander initially towards a broad region of the search space containing good solutions, ignoring small features of the energy function; then drift towards low-energy regions that become narrower and narrower; and finally move downhill according to the
steepest descent heuristic.







Chou–Fasman method

The Chou–Fasman method is an empirical technique for the prediction of
secondary structures in proteins, originally developed in the 1970s by Peter Y. Chou and Gerald D. Fasman.[1][2][3] The method is based on analyses of the relative frequencies of each amino acid in alpha helices, beta sheets, and
turns based on known
protein structures solved with
X-ray crystallography. From these frequencies a set of probability parameters were derived for the appearance of each amino acid in each secondary structure type, and these parameters are used to predict the probability that a given sequence of amino acids would form a helix, a beta strand, or a turn in a protein. The method is at most about 50–60% accurate in identifying correct secondary structures,[4] which is significantly less accurate than the modern
machine learning–based techniques.

Algorithm

The Chou–Fasman method predicts helices and strands in a similar fashion, first searching linearly through the sequence for a "nucleation" region of high helix or strand probability and then extending the region until a subsequent four-residue window carries a probability of less than 1. As originally described, four out of any six contiguous amino acids were sufficient to nucleate helix, and three out of any contiguous five were sufficient for a sheet. The probability thresholds for helix and strand nucleations are constant but not necessarily equal; originally 1.03 was set as the helix cutoff and 1.00 for the strand cutoff.
Turns are also evaluated in four-residue windows, but are calculated using a multi-step procedure because many turn regions contain amino acids that could also appear in helix or sheet regions. Four-residue turns also have their own characteristic amino acids; proline and glycine are both common in turns. A turn is predicted only if the turn probability is greater than the helix or sheet probabilities and a probability value based on the positions of particular amino acids in the turn exceeds a predetermined threshold. The turn probability p(t) is determined as:
p(t)=f(j)*f(j+1)*f(j+2)*f(j+3)
where f(j), f(j+1), f(j+2) and f(j+3) are bend frequencies in the four positions on the beta turn.
If:
p(t)>0.000075;
the average value for P(turn)>1.00 in the tetrapeptide where P(turn) is the conformational parameter for ß-turn ; and the averages for the tetrapeptide obey the inequality P(helix)<P(turn)>P(sheet), then a ß-turn is predicted at that location where P(helix) and P(sheet) are the conformational parameters for helix and sheet respectively.

Genetic algorithm

In the computer science field of artificial intelligence, a genetic algorithm (GA) is a
search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems.[1] Genetic algorithms belong to the larger class of evolutionary algorithms (EA), which generate solutions to optimization problems using techniques inspired by natural evolution, such as inheritance, mutation, selection, and crossover.

Methodology

In a genetic algorithm, a population of candidate solutions (called individuals, creatures, or phenotypes) to an optimization problem is evolved toward better solutions. Each candidate solution has a set of properties (its chromosomes or genotype) which can be mutated and altered; traditionally, solutions are represented in binary as strings of 0s and 1s, but other encodings are also possible.[2]
The evolution usually starts from a population of randomly generated individuals and happens in generations. In each generation, the fitness of every individual in the population is evaluated, the more fit individuals are stochastically selected from the current population, and each individual's genome is modified (recombined and possibly randomly mutated) to form a new population. The new population is then used in the next iteration of the algorithm. Commonly, the algorithm terminates when either a maximum number of generations has been produced, or a satisfactory fitness level has been reached for the population.
A typical genetic algorithm requires:
  1. a genetic representation of the solution domain,
  2. a fitness function to evaluate the solution domain.
A standard representation of each candidate solution is as an array of bits.[2] Arrays of other types and structures can be used in essentially the same way. The main property that makes these genetic representations convenient is that their parts are easily aligned due to their fixed size, which facilitates simple crossover operations. Variable length representations may also be used, but crossover implementation is more complex in this case. Tree-like representations are explored in
genetic programming and graph-form representations are explored in evolutionary programming; a mix of both linear chromosomes and trees is explored in gene expression programming.
Once the genetic representation and the fitness function are defined, a GA proceeds to initialize a population of solutions and then to improve it through repetitive application of the mutation, crossover, inversion and selection operators.

[edit] Initialization

Initially many individual solutions are (usually) randomly generated to form an initial population. The population size depends on the nature of the problem, but typically contains several hundreds or thousands of possible solutions. Traditionally, the population is generated randomly, allowing the entire range of possible solutions (the search space). Occasionally, the solutions may be "seeded" in areas where optimal solutions are likely to be found.

[edit] Selection

During each successive generation, a proportion of the existing population is selected to breed a new generation. Individual solutions are selected through a fitness-based process, where
fitter solutions (as measured by a
fitness function) are typically more likely to be selected. Certain selection methods rate the fitness of each solution and preferentially select the best solutions. Other methods rate only a random sample of the population, as the former process may be very time-consuming.
The fitness function is defined over the genetic representation and measures the quality of the represented solution. The fitness function is always problem dependent.

[edit] Genetic operators

The next step is to generate a second generation population of solutions from those selected through
genetic operators: crossover (also called recombination), and/or mutation.
For each new solution to be produced, a pair of "parent" solutions is selected for breeding from the pool selected previously. By producing a "child" solution using the above methods of crossover and mutation, a new solution is created which typically shares many of the characteristics of its "parents". New parents are selected for each new child, and the process continues until a new population of solutions of appropriate size is generated. Although reproduction methods that are based on the use of two parents are more "biology inspired", some research[3][4] suggests that more than two "parents" generate higher quality chromosomes.

[edit] Termination

This generational process is repeated until a termination condition has been reached. Common terminating conditions are:
  • A solution is found that satisfies minimum criteria
  • Fixed number of generations reached
  • Allocated budget (computation time/money) reached
  • The highest ranking solution's fitness is reaching or has reached a plateau such that successive iterations no longer produce better results
  • Manual inspection
  • Combinations of the above





















Smith-Waterman Algorithm

The Smith-Waterman algorithm is a database search algorithm developed by T.F. Smith and M.S. Waterman, and based on an earlier model appropriately named Needleman and Wunsch after its original creators. The S-W Algorithm implements a technique called dynamic programming, which takes alignments of any length, at any location, in any sequence, and determines whether an optimal alignment can be found. Based on these calculations, scores or weights are assigned to each character-to-character comparison: positive for exact matches/substitutions, negative for insertions/deletions. In weight matrices, scores are added together and the highest scoring alignment is reported.
To put it simply, dynamic programming finds solutions to smaller pieces of the problem and then puts them all together to form a complete and optimal final solution to the entire problem.
It is superior to the BLAST and FASTA algorithms because it searches a larger field of possibilities, making it a more sensitive technique; however, individual pair-wise comparisons between letter slows the process down significantly.
Instead of looking at an entire sequence at once, the S-W algorithm compares multi-lengthed segments, looking for whichever segment maximizes the scoring measure. The algorithm itself is recursive in nature:
H i j = max{H i-1, j-1 + s(a i, b j ); H i-k, j - W k ; H i, j-1 - W 1 ;0}
So what are we doing?

In essence, we are converting one string (sequence of letters) into another string by performing certain operations on the individual characters that make up that string. We can insert a character or delete a character from the first string, or we can substitute a character in the first string with a character from the second string. Thus, an insertion into one string results in the simultaneous deletion from the second string. What we call an edit distance, is just the minimum number of operations we perform to convert one string into another. So the similarity of two strings is simply the value of the alignment between the two strings that maximizes the total alignment value (optimal alignment value), or the highest score given. Then how do we start figuring out the alignment? Global alignment is obtained by first inserting chosen spaces (or dashes) either into or at the ends of the two strings, and then placing the two resulting strings one above the other so that every character or space in either string is opposite a unique character or a unique space in the other string.
Let's say we have the sequence GAGTCGC and CTATGCA. We first line them up and compare the edit distance. Count the number of r's and d's (which in this case is 5) and that is the edit distance, while the number of m's is the similarity score (which equals 4).
                      G - A G T C G C -
                      r i m d m d m m i
                      C T A - T - G C A
for edit distance scoring,
r = replacement = 1
m = match = 0
i, d = insertion/deletion = 1
for similarity scoring,
m = matches = 1 and the rest are 0
edit distance = 5
similarity = 4
two strings are compared
A = a1 a2 ... an
B = b1 b2 ... bm
similarity s(a,b)
is given by a weight matrix
first term
corresponds to extending the alignment by one residue from each sequence
second term
describes extending the alignment by including a residue from sequence (string) b and inserting a gap of k residues in length, aligned to end with a residue of sequence (string) b, into sequence a
third term
same as inserting a gap into sequence b
fourth term
0, allows for partial scores within the table to become negative
putting zero in the recursion accounts for the case that if the alignment score becomes negative, it is ignored and the preceding calculations are ignored as well, and start over from a neutral score
matrix
first fill with zeros
calculate H i j
where W k = 1 + (1/3) * k and k = gap length
choose the highest score
there are only four possible ways to forming a path:
  1. align with next residue of database sequence (score is previous score plus similarity score for the two residues
  2. deletion
  3. insertion
  4. zero
From the scoring matrix, the S-W algorithm finds the highest score and traces back the path of the previous highest scores. This in essence determines the places in the query sequence in which to place dashes (insertions or deletions). The calculated path can then report to the user the sequence in the database that best matches the query string.

Expectation–maximization algorithm

In statistics, an expectation–maximization (EM) algorithm is an
iterative method for finding
maximum likelihood or
maximum a posteriori (MAP) estimates of parameters in
statistical models, where the model depends on unobserved
latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step.

Properties

Speaking of an expectation (E) step is a bit of a misnomer. What is calculated in the first step are the fixed, data-dependent parameters of the function Q. Once the parameters of Q are known, it is fully determined and is maximized in the second (M) step of an EM algorithm.
Although an EM iteration does increase the observed data (i.e. marginal) likelihood function there is no guarantee that the sequence converges to a maximum likelihood estimator. For
multimodal distributions, this means that an EM algorithm may converge to a local maximum of the observed data likelihood function, depending on starting values. There are a variety of heuristic or metaheuristic approaches for escaping a local maximum such as random restart (starting with several different random initial estimates θ(t)), or applying simulated annealing methods.
EM is particularly useful when the likelihood is an exponential family: the E step becomes the sum of expectations of sufficient statistics, and the M step involves maximizing a linear function. In such a case, it is usually possible to derive closed form updates for each step, using the Sundberg formula (published by Rolf Sundberg using unpublished results of Per Martin-Löf and
Anders Martin-Löf).[3][4][7][8][9][10][11]
The EM method was modified to compute
maximum a posteriori (MAP) estimates for Bayesian inference in the original paper by Dempster, Laird, and Rubin.
There are other methods for finding maximum likelihood estimates, such as gradient descent,
conjugate gradient or variations of the Gauss–Newton method. Unlike EM, such methods typically require the evaluation of first and/or second derivatives of the likelihood function.

Applications

EM is frequently used for
data clustering in
machine learning and
computer vision. In natural language processing, two prominent instances of the algorithm are the Baum-Welch algorithm (also known as forward-backward) and the inside-outside algorithm for unsupervised induction of probabilistic context-free grammars.
In psychometrics, EM is almost indispensable for estimating item parameters and latent abilities of
item response theory models.
With the ability to deal with missing data and observe unidentified variables, EM is becoming a useful tool to price and manage risk of a portfolio.
The EM algorithm (and its faster variant Ordered subset expectation maximization) is also widely used in
medical image reconstruction, especially in positron emission tomography and single photon emission computed tomography.


















Hidden Markov model

A hidden Markov model (HMM) is a
statistical Markov model in which the system being modeled is assumed to be a
Markov process with unobserved (hidden) states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by
L. E. Baum and coworkers.[1][2][3][4][5] It is closely related to an earlier work on optimal nonlinear filtering problem (stochastic processes) by
Ruslan L. Stratonovich,[6] who was the first to describe the forward-backward procedure.
In simpler Markov models (like a Markov chain), the state is directly visible to the observer, and therefore the state transition probabilities are the only parameters. In a hidden Markov model, the state is not directly visible, but output, dependent on the state, is visible. Each state has a probability distribution over the possible output tokens. Therefore the sequence of tokens generated by an HMM gives some information about the sequence of states. Note that the adjective 'hidden' refers to the state sequence through which the model passes, not to the parameters of the model; even if the model parameters are known exactly, the model is still 'hidden'.
Hidden Markov models are especially known for their application in temporal pattern recognition such as
speech, handwriting,
gesture recognition,[7] part-of-speech tagging, musical score following,[8]
partial discharges[9] and bioinformatics.
A hidden Markov model can be considered a generalization of a mixture model where the hidden variables (or
latent variables), which control the mixture component to be selected for each observation, are related through a Markov process rather than independent of each other.

Description in terms of urns

Figure 1. Probabilistic parameters of a hidden Markov model (example)
x — states
y — possible observations
a — state transition probabilities
b — output probabilities
In its discrete form, a hidden Markov process can be visualized as a generalization of the Urn problem[10]: In a room that is not visible to an observer there is a genie. The room contains urns X1, X2, X3, ... each of which contains a known mix of balls, each ball labeled y1, y2, y3, ... . The genie chooses an urn in that room and randomly draws a ball from that urn. It then puts the ball onto a conveyor belt, where the observer can observe the sequence of the balls but not the sequence of urns from which they were drawn. The genie has some procedure to choose urns; the choice of the urn for the n-th ball depends only upon a random number and the choice of the urn for the (n − 1)-th ball. The choice of urn does not directly depend on the urns chosen before this single previous urn; therefore, this is called a
Markov process. It can be described by the upper part of Figure.

Applications

HMMs can be applied in many fields where the goal is to recover a data sequence that is not immediately observable (but other data that depends on the sequence is). Applications include:









Needleman–Wunsch algorithm

The Needleman–Wunsch algorithm performs a global alignment on two sequences (called A and B here). It is commonly used in bioinformatics to align protein or nucleotide sequences. The algorithm was published in 1970 by Saul B. Needleman and Christian D. Wunsch.[1]
The Needleman–Wunsch algorithm is an example of
dynamic programming, and was the first application of dynamic programming to biological sequence comparison. It is sometimes referred to as the
Optimal matching algorithm.

A modern presentation

Scores for aligned characters are specified by a
similarity matrix. Here, is the similarity of characters a and b. It uses a linear gap penalty, here called d.
For example, if the similarity matrix was

A
G
C
T
A
10
-1
-3
-4
G
-1
7
-5
-3
C
-3
-5
9
0
T
-4
-3
0
8
then the alignment:
AGACTAGTTAC
CGA‒‒‒GACGT
with a gap penalty of -5, would have the following score:


To find the alignment with the highest score, a two-dimensional
array (or matrix) F is allocated. The entry in row i and column j is denoted here by . There is one column for each character in sequence A, and one row for each character in sequence B. Thus, if we are aligning sequences of sizes n and m, the amount of memory used is in . Hirschberg's algorithm only holds a subset of the array in memory and uses space, but is otherwise similar to Needleman-Wunsch (and still requires time).
As the algorithm progresses, the will be assigned to be the optimal score for the alignment of the first characters in A and the first characters in B. The principle of optimality is then applied as follows:
  • Basis:


  • Recursion, based on the principle of optimality:













STEPS INVOLVED IN DRUG DESIGNING
Drug designing basically of two types namely ligand based approach or receptor based approach.  In both the case the point of centre only differ but requirement of receptor and ligand essential in both the case.  By considering these facts, the following steps shown below for drug designing.
Drug designing steps were usually divided into steps as follows:
I. LIGAND PREPARATION
II. RECEPTOR PREPARATION
III. DOCKING
IV. BINDING AFFINITY STUDIES
1. LIGAND PREPARATION:
Ligand preparation further divided into different heading namely, ligand retrieval or collection, liand conversion and ligand analysis.
The DrugBank database is a unique bioinformatics and cheminformatics resource that combines detailed drug (i.e. chemical, pharmacological and pharmaceutical) data with comprehensive drug target (i.e. sequence, structure, and pathway) information.
Molecular descriptors plays crucial role in the drug identification area.  So it is essential to know and have the molecular descriptors values regarding ligands.  Molecular descriptors predicted through QSAR and QPAR models.
II. RECEPTOR PREPARATION:
For drug to act, target is necessary which might be of receptor or enzyme or hormone type.  Initially, the receptor should  be prepared by structure modeling method or it might be download from the structure databases.  After modeling or downloading from corresponding sources, it should be prepared properly for docking which might be achieved by using binding site analysis tools and target determination tools.
III. DOCKING:
After collecting, preparing ligands and receptors, they should be assessed for their interaction ability with docking procedure. Docking studied under two heads namely, protein-ligand docking and protein-protein docking.


IV. BINDING AFFINITY STUDIES:


AffinDB is a database of affinity data for structurally resolved protein–ligand complexes from the Protein Data Bank (PDB). Affinity data are collected from the scientific literature, both from primary sources describing the original experimental work of affinity determination and from secondary references which report affinity values determined by others.
In computational structure-based drug design, the scoring functions are the cornerstones to the success of design/discovery. Many approaches have been explored to improve their reliability and accuracy, leading to three families of scoring functions: force-field-based, knowledge-based, and empirical. The last family is the most widely used in association with docking algorithms because of its speed, even though such empirical scoring functions produce far too many false positives to be fully reliable.

Posted by at

No comments:

Post a Comment

Note: Only a member of this blog may post a comment.

Subscribe to: Post Comments (Atom)